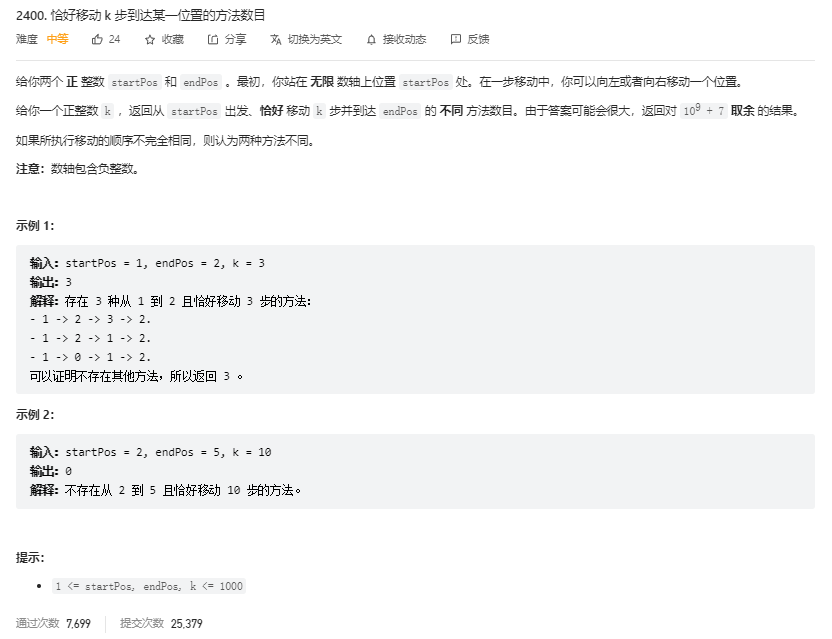
题目分析
本题是周赛的第二题,有两种思路,虽然是一个mid题目,但是我觉得难度还是相当大的,小伙伴们能否想出$ O(n^2) $的解法呢,能否再进一步想出更优的解法呢?
动态规划
这个题目动态规划其实不容易想到,因为动态规划的时间复杂度较高,所以我先讲解DP。
可以用一个二维的DP来表示,dp[i][j]表示经过i步到达j位置的走法。因此有下面的状态转移方程
$$ dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1] $$
此题要注意的是,位置可能是负数,因此需要先加上某个值,让其变为正数。
因为k <= 1000,因此最多移动到-500的位置,就必须往回走了,所以我们只需要+500即可。
因此移动的范围是(-500-1500],算法的时间复杂度为$ O(n^2) $,空间复杂度为O(n^2)。
1 | class Solution { |
数学
本题的最优解是使用组合数,我们想一共需要走k步,他们之间的距离是d,因此我们需要左右分别走(k - d) / 2步,即向左走(k - d) / 2步,再向右走(k - d) / 2步。
所以问题的本质是从k步中选择向终点方向走d + (k - d)步,因此就变成了计算$ C^{d + (k - d)}_k $ 的值。可以利用公式
$$ C^n_m = C^{n - 1}{m - 1} + C^n{m - 1} $$
然后递推求解,递推的过程也是一种DP,算法的时间复杂度为$ O(n^2) $,空间复杂度为O(n^2)。
1 | class Solution { |
这种做法虽然比普通的DP快一些,因为没有+500的时空复杂度。但是还是$ O(n^2) $的。
我们可以根据组合数的数学表达式入手
$$ C^n_m = \frac{m!}{(m - n)! \times n!} $$
此时小伙伴们犯难了,我们已知
$$ (a + b) % p = ((a % p) + (b % p)) % p $$
$$ (a - b) % p = ((a % p) - (b % p)) % p $$
$$ (a \times b) % p = ((a % p) \times (b % p)) % p $$
但是除法是不成立的,那应该怎么办呢?
如果能将除法变成乘法,那么本题不就是求阶乘的题目吗?是可以做到$ O(n) $的复杂度。
我们可以考虑一下逆元的思想,何为逆元?
假设a x b % p = 1,则我们称b为a % p的逆元。逆元有什么性质呢?
逆元最重要的一点是(m / a) % p 等价于(m x b) % p,下面给大家进行证明
$$ \frac{m}{a} % p = \frac{m}{a} % p \times 1 = \frac{m}{a} % p \times (a \times b) % p = (m \times b) % p $$
所以我们要求
$$ \frac{m!}{(m - n)! \times n!} $$
就等价于求(m - n)! x n!的逆元。
下面问题又来了,如何求解某个数的逆元呢?
根据费马小定理
$$ a^{p - 1} % p = 1, p为质数$$
因此可以得出下面公式
$$ (a \times a^{p - 2}) % p = 1 $$
说明$ a^{p - 2} $是a的逆元。因此问题转化为求$ x^{p - 2} $,根据快速幂的思想,可以在O(log(n))的时间复杂度内求出。我们绕了半天,先讲解了组合数公式、又讲解了逆元、又到费马小定理、最后到快速幂。其实代码的实现非常简单,比DP的代码还要少。
1 | class Solution { |
刷题总结
组合数在刷题中经常能遇到,希望大家能学会逆元法求解组合数的思想。感兴趣也可以去扩展一下卢卡斯定理。$$ C^n_m % p = (C^{n % p}{m % p} \times C^{n / p}{m / p}) % p $$,当m较大时,求解阶乘较慢,可以使用卢卡斯定理。